众所周知,收集问卷是个受累不讨好的活,在过去线下收集问卷自然是非常麻烦,而线上问卷收集依然不是一个非常轻松的活。就以我个人为例,扩大到最大的影响力也不过是收集到了 155 份问卷,而且这个问卷还是以单选题为主。

自然就有人动歪脑筋,反正最后也是算一个百分比,把数字按比例扩大,百分比照样不变,还能显出自己的工作量之大,计算量也小了不少,可谓是两难自解。
但是,古尔丹,代价是什么呢?
互质#
让我们引入一个简单的概念 —— 互质。
若两个非零整数的最大公约数为 1(即它们的公因数只有 1),则称这两个数互质。互质有一些非常有趣的性质
- 与 1 的关系 :1 与任何整数互质,因为 1 的因数只有自身。
- 质数特性 :不同质数必然互质,如 3 和 5。
- 相邻数规律 :相邻的两个自然数(如 8 和 9)或相邻奇数(如 15 和 17)一定互质。
- 判断方法 :可以通过计算最大公约数(如欧几里得算法)判断两个数是否互质。
如果把数字按比例扩大,分子分母同时扩大,虽然百分比不变,但是分子与分母就必然不可能互质。或者反过来说,只要找到一对互质的数,使得相除后的结果接近算出的百分比,就可以大致得出真实的问卷数量,任何放缩,必将绳之以法!
如何操作#
我们假设问卷数为,百分比大小为,对应的分子为,即,一般百分比保留两位小数,所以我们的精度必须小于,每一个与都是整数,所以我们就可以带入一些数字硬算了。
当然也可以培养一下对于数字的敏感性,简单点说可以关注的值,的分子分母必然互质,属于是非常显眼的特征。比如说看到就差不多能猜测问卷一共只有 3 份,估计是自己填了一份,自己朋友填一份,再找异性填一份,还可以兼顾性别比例。
深一点想的话,看到 0.0222、0.1556、0.1778、0.4667 就能迅速反应过来这些数是
言及于此,不由得感慨这个问题实在是简简又单单啊,稍微一瞪眼就看出来结果了,so easy 啊,写了这么长,文章也该结束了吧?
那当然不可能,感谢 AI,完善了我的思路,甚至更进一步,实在是好上加好,解放了我的大脑,思路非常简单,数字也不是很大,暴力就得了。
import math
from itertools import product
from functools import reduce
def find_min_n_direct(decimal_list, tolerance=0.0001, max_n=10000):
"""
直接搜索法:从小到大尝试每个整数n,直到找到符合条件的最小值
参数:
decimal_list: 小数列表
tolerance: 误差容忍度,相对于n的值
max_n: 搜索的最大n值
返回:
满足条件的最小整数n,如果未找到则返回None
"""
for n in range(1, max_n + 1):
valid = True
for x in decimal_list:
k = round(x * n)
error = abs(x * n - k) / n
if error > tolerance:
valid = False
break
if valid:
return n
return None
# 用户输入
m = int(input("请输入小数的个数 m: "))
decimals = [float(input(f"请输入第 {i+1} 个小数: ")) for i in range(m)]
# 执行搜索
result = find_min_n_direct(decimals)
# 输出结果
if result:
print(f"满足条件的最小整数 n = \033[1;32m{result}\033[0m")
# 打印详细信息
print("\n验证结果:")
for x in decimals:
k = round(x * result)
error = abs(x * result - k)
print(f"{x} × {result} = {x*result:.4f} ≈ {k} (误差: {error:.4f})")
else:
print("未找到符合条件的 n。")
到了这里就要结束了吗?当然不会,肯定有人会说如果我的问卷的数据非常恰好,就是没有任何一个分子与总问卷数互质,这样算出来的数据就会小于总问卷数,没有参考性。
如果这样的话,那只能说是非常巧了,我们就需要引入另一个概念了。
欧拉函数#
欧拉函数(Euler's totient function),记作 (),是数论中用于计算小于等于正整数且与互质的正整数的数目的函数.
定义#
对正整数,表示在到之间与互质的数的个数。例如:
-
,因为与互质。
-
,因为与互质。
-
特殊值:,因为与自身互质。
核心性质#
- 积性函数
若与互质,则。
- 质数的欧拉函数
若为质数,则,因为所有小于的数均与互质。
- 质数幂次的欧拉函数
若为质数,为正整数,则。
例如,。
- 通用计算公式
若的质因数分解为,则:
例如,,则:
图像#
欧拉函数的图像大致是这个样子。
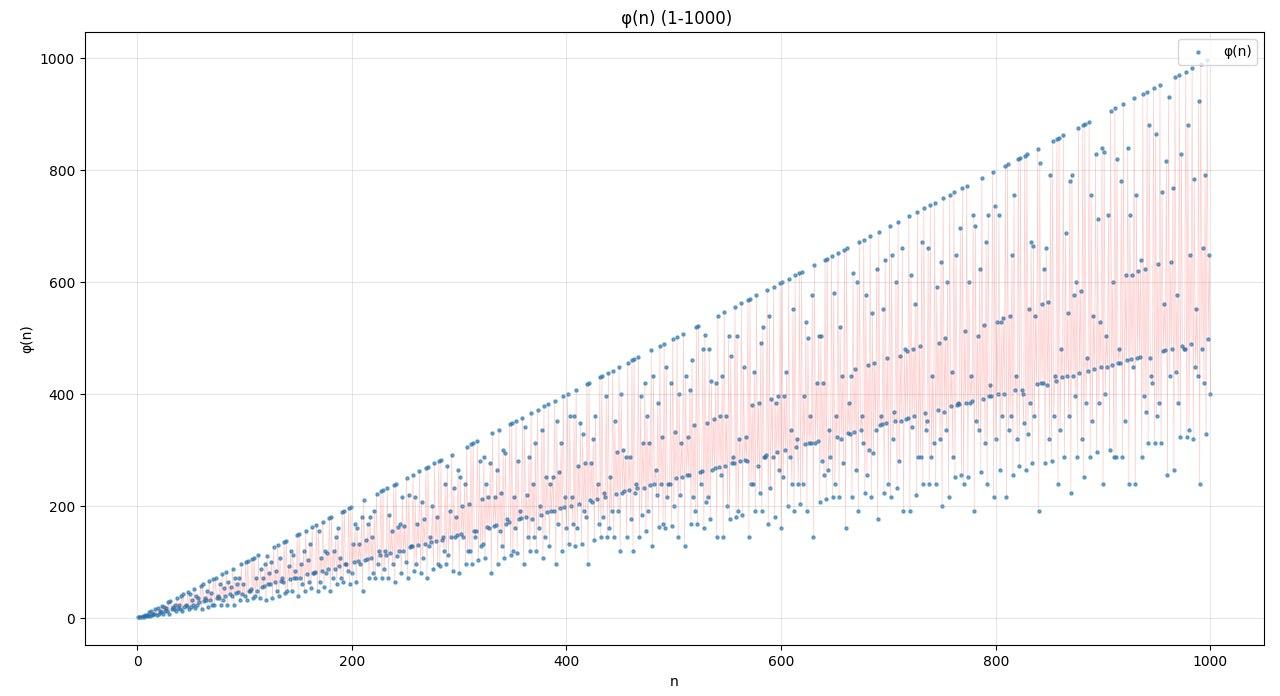
若的质因数分解为,根据这个公式可以通过以下的代码画出这个函数
import matplotlib.pyplot as plt
import numpy as np
def euler_phi(n):
"""计算欧拉函数φ(n):小于或等于n且与n互质的正整数的个数"""
result = n # 初始化为n
# 检查所有可能的质因数
p = 2
while p * p <= n:
if n % p == 0:
# p是n的一个质因数
while n % p == 0:
n //= p
result -= result // p # φ(n) = φ(n) * (1 - 1/p)
p += 1
# 如果n最后大于1,则n是一个质数
if n > 1:
result -= result // n
return result
# 计算从1到1000的欧拉函数值
n_values = np.arange(1, 1001)
phi_values = [euler_phi(n) for n in n_values]
# 创建图像
plt.figure(figsize=(12, 8))
plt.scatter(n_values, phi_values, s=5, alpha=0.6) # 减小点的大小,增加可读性
plt.plot(n_values, phi_values, 'r-', alpha=0.2, linewidth=0.5) # 淡化连线
# 添加图像标题和标签
plt.title(' φ(n) (1-1000)')
plt.xlabel('n')
plt.ylabel('φ(n)')
plt.grid(True, alpha=0.3)
plt.legend(['φ(n)'], loc='upper right')
# 显示图像
plt.tight_layout()
plt.show()
通过图像,不难看出
的取值为整数,图像由离散点组成,但通常以折线或散点图形式呈现连续趋势
为质数时,图像中沿直线 分布的,如时。
为幂次合数时,如,,值较高但低于同范围质数。
为多质因数合数时,如,,远低于相邻质数点。
的特点#
当然,我们还可以更进一步,看看调查问卷数据有多大可能击中一对非互质的分子分母。还是老性质,若 $n$ 的质因数分解为,则:。
那么就有
那么就很简单了,假设问卷数 $n$ 的质因数有,那么与随机碰撞到互质的分子分母的概率是相同的,如果有谁的问卷的数据非常恰好,就是没有任何一个分子与总问卷数()互质,那么在更大的数据范围内也有相同的概率就是没有任何一个分子与总问卷数()互质。既然概率相同,你怎么专挑这件事情报道,因此前文所述的情况,明显是可能性很小的。我们这里也不是刑法,不需要保持什么谦益性,这种概率非常小的情况完全可以忽略。
假设不是问卷数的质因数,那么与随机碰撞到互质的分子分母的概率就大有不同,可以看看的质因数,找几个并非的质因数,与乘起来看看咸淡,挑一个比较合理的就可以。
但是大家也不用因此沮丧,还是看看图像吧。
就有以下的图像
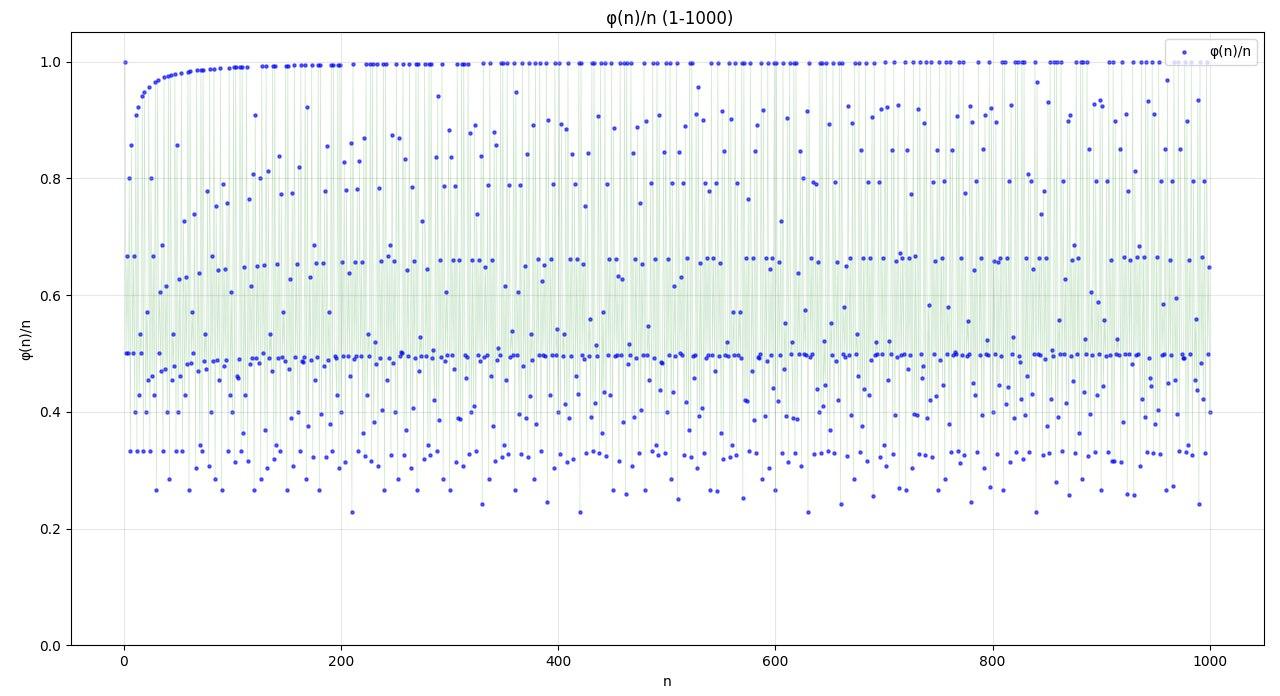
或许范围可以大一些
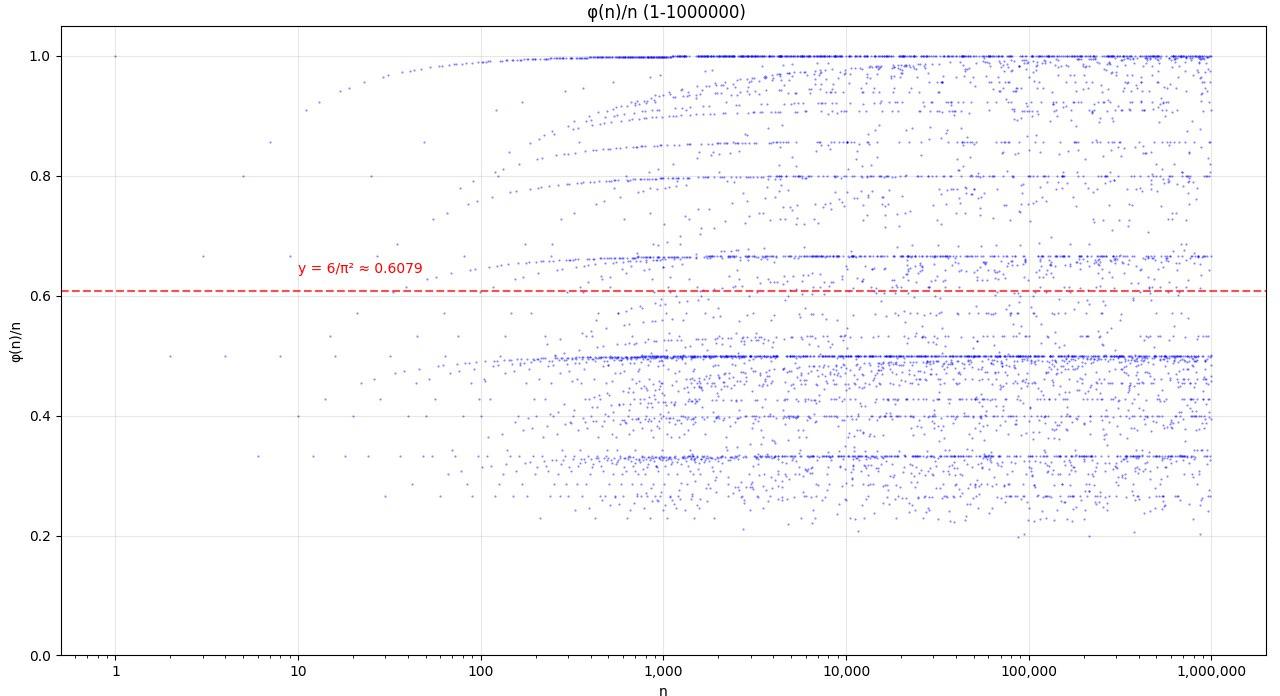
这样看得就清楚多了。
可以看到,图像呈现明显的分形特性和自相似模式,可以观察到多个周期性下降的结构,每条 "支线" 对应特定质数的倍数,随着 n 增大,整体趋势呈下降波动,而且随着 n 增大,φ(n)/n 的平均值趋近于 6/π² ≈ 0.6079,这个结果与素数分布的渐近密度相关。(以上是 AI 生成)
由此可见,既然碰撞概率下降不明显,总而言之这个方法还是比较可信的,可以轻松发现一些没什么诚意的造假。
缺陷#
当然这个方法也是有缺陷的,出了上文提到的不严谨之处,由于通常的问卷调查结果是保留两位小数的百分数,所以本代码对误差的 tolerance 在 0.0001,如果问卷数量超过 10000 份,得出的结果也只有 10000,能力就限制到这儿了。如果结果是保留一位小数的百分数,tolerance 在 0.001,那就是上限 1000 份,以此类推了。
此外穷举优雅性不足,本来让 AI 写了一个连分数的算法,结果没过测试,部分情况算出来的数字偏大,反正只有 10000 个数字,都用 python 了,就别追求效率,穷举就完了。
最后还有一个缺陷,但我是不会说的,那不是增加我的发现难度吗!
最后用一些知网的文献练练手,让大家看看到底准不准。






OK,收工。
此文由 Mix Space 同步更新至 xLog
原始链接为 https://www.actorr.cn/posts/default/Eulerstotient