HeQihan

眾所周知，收集問卷是個受累不討好的活，在過去線下收集問卷自然是非常麻煩，而線上問卷收集依然不是一個非常輕鬆的活。就以我個人為例，擴大到最大的影響力也不過是收集到了 155 份問卷，而且這個問卷還是以單選題為主。

自然就有人動歪腦筋，反正最後也是算一個百分比，把數字按比例擴大，百分比照樣不變，還能顯出自己的工作量之大，計算量也小了不少，可謂是兩難自解。

但是，古爾丹，代價是什麼呢？

互質#

讓我們引入一個簡單的概念 —— 互質。

若兩個非零整數的最大公約數為 1（即它們的公因數只有 1），則稱這兩個數互質。互質有一些非常有趣的性質

• 與 1 的關係 ：1 與任何整數互質，因為 1 的因數只有自身。
• 質數特性 ：不同質數必然互質，如 3 和 5。
• 相鄰數規律 ：相鄰的兩個自然數（如 8 和 9）或相鄰奇數（如 15 和 17）一定互質。
• 判斷方法 ：可以通過計算最大公約數（如歐幾里得算法）判斷兩個數是否互質。

如果把數字按比例擴大，分子分母同時擴大，雖然百分比不變，但是分子與分母就必然不可能互質。或者反過來說，只要找到一對互質的數，使得相除後的結果接近算出的百分比，就可以大致得出真實的問卷數量，任何放縮，必將繩之以法！

如何操作#

我們假設問卷數為$N$，百分比大小為$a_1,a_2,a_3,\cdots a_n$，$a_1,a_2,a_3,\cdots a_n$對應的分子為$b_1,b_2,b_3,\cdots b_n$，即$a_1\approx\frac{b_1}{N},a_2\approx\frac{b_2}{N}\cdots a_n\approx\frac{b_n}{N}$，一般百分比保留兩位小數，所以我們的精度必須小於$0.0001$，每一個$b_1$與$N$都是整數，所以我們就可以帶入一些數字硬算了。

當然也可以培養一下對於數字的敏感性，簡單點說可以關注$\frac{1}{某數}$的值，$\frac{1}{某數}$的分子分母必然互質，屬於是非常顯眼的特徵。比如說看到$\frac{1}{3}$就差不多能猜測問卷一共只有 3 份，估計是自己填了一份，自己朋友填一份，再找異性填一份，還可以兼顧性別比例。

深一點想的話，看到 0.0222、0.1556、0.1778、0.4667 就能迅速反應過來這些數是

言及於此，不由得感慨這個問題實在是簡簡又單單啊，稍微一瞪眼就看出來結果了，so easy 啊，寫了這麼長，文章也該結束了吧？

那當然不可能，感謝 AI，完善了我的思路，甚至更進一步，實在是好上加好，解放了我的大腦，思路非常簡單，數字也不是很大，暴力就得了。

import math

from itertools import product

from functools import reduce

  

def find_min_n_direct(decimal_list, tolerance=0.0001, max_n=10000):

    """

    直接搜索法：從小到大嘗試每個整數n，直到找到符合條件的最小值

    參數:

        decimal_list: 小數列表

        tolerance: 誤差容忍度，相對於n的值

        max_n: 搜索的最大n值

    返回:

        滿足條件的最小整數n，如果未找到則返回None

    """

    for n in range(1, max_n + 1):

        valid = True

        for x in decimal_list:

            k = round(x * n)

            error = abs(x * n - k) / n

            if error > tolerance:

                valid = False

                break

        if valid:

            return n

    return None

  

# 用戶輸入

m = int(input("請輸入小數的個數 m: "))

decimals = [float(input(f"請輸入第 {i+1} 個小數: ")) for i in range(m)]

  

# 執行搜索

result = find_min_n_direct(decimals)

  

# 輸出結果

if result:

    print(f"滿足條件的最小整數 n = \033[1;32m{result}\033[0m")

    # 打印詳細信息

    print("\n驗證結果:")

    for x in decimals:

        k = round(x * result)

        error = abs(x * result - k)

        print(f"{x} × {result} = {x*result:.4f} ≈ {k} (誤差: {error:.4f})")

else:

    print("未找到符合條件的 n。")

到了這裡就要結束了嗎？當然不會，肯定有人會說如果我的問卷的數據非常恰好，就是沒有任何一個分子與總問卷數互質，這樣算出來的數據就會小於總問卷數，沒有參考性。

如果這樣的話，那只能說是非常巧了，我們就需要引入另一個概念了。

歐拉函數#

歐拉函數（Euler's totient function），記作 ($\varphi(n)$)，是數論中用於計算小於等於正整數$n$且與$n$互質的正整數的數目的函數.

定義#

對正整數$n$，$\varphi(n)$表示在$1$到$n$之間與$n$互質的數的個數。例如：

• $\varphi(8) = 4$，因為$1, 3, 5, 7$與$8$互質。

• $\varphi(12) = 4$，因為$1, 5, 7, 11$與$12$互質。

• 特殊值：$\varphi(1) = 1$，因為$1$與自身互質。

核心性質#

1. 積性函數 

   若$a$與$b$互質，則$\varphi(ab) = \varphi(a)\varphi(b)$。

2. 質數的歐拉函數 

   若$p$為質數，則$\varphi(p) = p-1$，因為所有小於$p$的數均與$p$互質。

3. 質數幂次的歐拉函數 

   若$p$為質數，$k$為正整數，則$\varphi(p^k) = p^k - p^{k-1}$。 

   例如，$\varphi(9) = \varphi(3^2) = 9 - 3 = 6$。

4. 通用計算公式 

   若$n$的質因數分解為$n = p_1^{k_1} p_2^{k_2} \cdots p_m^{k_m}$，則：

   例如，$n = 12 = 2^2 \cdot 3^1$，則：

圖像#

歐拉函數的圖像大致是這樣的。

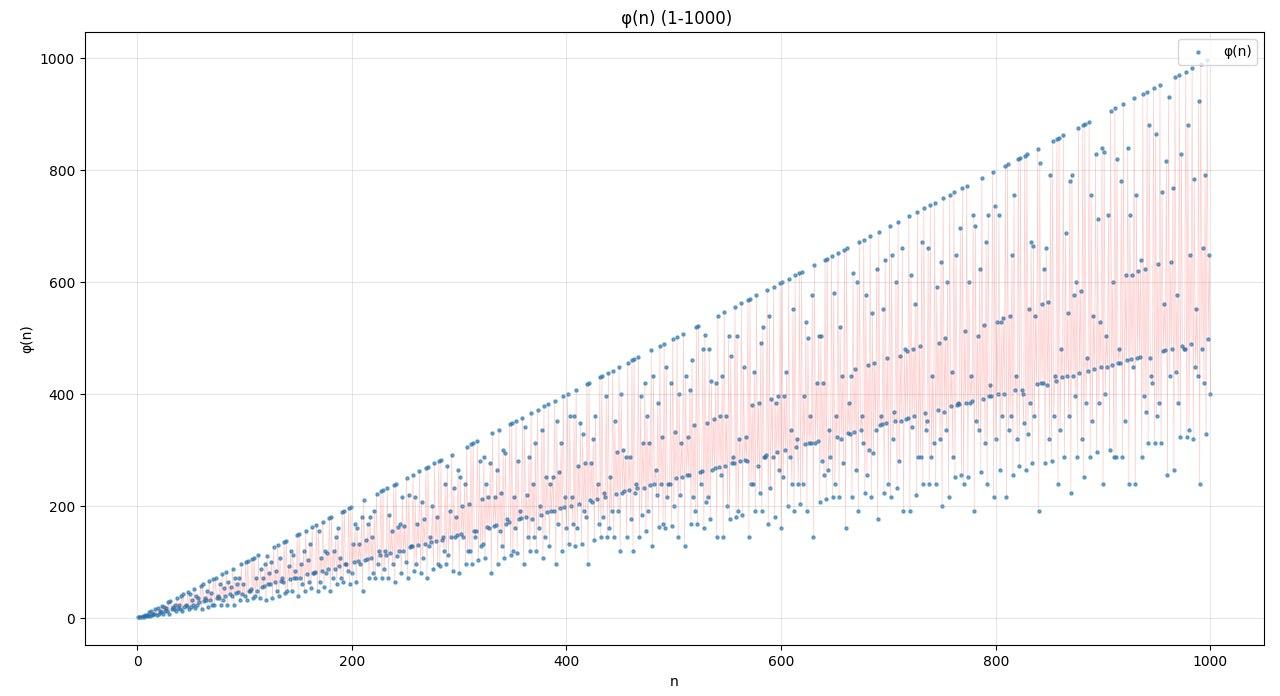
若$n$的質因數分解為$n = p_1^{k_1} p_2^{k_2} \cdots p_m^{k_m}$，根據$\varphi(n) = n \left(1 - \frac{1}{p_1}\right)\left(1 - \frac{1}{p_2}\right) \cdots \left(1 - \frac{1}{p_m}\right)$這個公式可以通過以下的代碼畫出這個函數

import matplotlib.pyplot as plt

import numpy as np

  

def euler_phi(n):

    """計算歐拉函數φ(n)：小於或等於n且與n互質的正整數的個數"""

    result = n  # 初始化為n

    # 檢查所有可能的質因數

    p = 2

    while p * p <= n:

        if n % p == 0:

            # p是n的一个質因數

            while n % p == 0:

                n //= p

            result -= result // p  # φ(n) = φ(n) * (1 - 1/p)

        p += 1

    # 如果n最後大於1，則n是一個質數

    if n > 1:

        result -= result // n

    return result

  

# 計算從1到1000的歐拉函數值

n_values = np.arange(1, 1001)

phi_values = [euler_phi(n) for n in n_values]

  

# 創建圖像

plt.figure(figsize=(12, 8))

plt.scatter(n_values, phi_values, s=5, alpha=0.6)  # 減小點的大小，增加可讀性

plt.plot(n_values, phi_values, 'r-', alpha=0.2, linewidth=0.5)  # 淡化連線

  

# 添加圖像標題和標籤

plt.title(' φ(n) (1-1000)')

plt.xlabel('n')

plt.ylabel('φ(n)')

plt.grid(True, alpha=0.3)

  
  

plt.legend(['φ(n)'], loc='upper right')

  

# 顯示圖像

plt.tight_layout()

plt.show()

通過圖像，不難看出

$\varphi(n)$ 的取值為整數，圖像由離散點組成，但通常以折線或散點圖形式呈現連續趨勢

$n$為質數時$\varphi(p) = p-1$，圖像中沿直線 $y = x-1$ 分佈的，如$n=11$時$\varphi(11)=10$。

$n$為幂次合數時，如$n=9=3^2$，$\varphi(9)=6$，值較高但低於同範圍質數。

$n$為多質因數合數時，如$n=30=2 \cdot 3 \cdot 5$，$\varphi(30)=8$，遠低於相鄰質數點。

$\frac{\varphi(n)}{n}$的特點#

當然，我們還可以更進一步，看看調查問卷數據有多大可能擊中一對非互質的分子分母。還是老性質，若 $n$ 的質因數分解為$n = p_1^{k_1} p_2^{k_2} \cdots p_m^{k_m}$，則：$\varphi(n) = n \left(1 - \frac{1}{p_1}\right)\left(1 - \frac{1}{p_2}\right) \cdots \left(1 - \frac{1}{p_m}\right)$。

那麼就有$\frac{\varphi(n)}{n} = \left(1 - \frac{1}{p_1}\right)\left(1 - \frac{1}{p_2}\right) \cdots \left(1 - \frac{1}{p_m}\right)$

那麼就很簡單了，假設問卷數 $n$ 的質因數有$p_m$，那麼$p_m \times n$與$n$隨機碰撞到互質的分子分母的概率是相同的，如果有誰的問卷的數據非常恰好，就是沒有任何一個分子與總問卷數（$p_m \times n$）互質，那麼在更大的數據範圍內也有相同的概率就是沒有任何一個分子與總問卷數（$n$）互質。既然概率相同，你怎麼專挑這件事情報導，因此前文所述的情況，明顯是可能性很小的。我們這裡也不是刑法，不需要保持什麼謙益性，這種概率非常小的情況完全可以忽略。

假設$p_l$不是問卷數$n$的質因數，那麼$p_l \times n$與$n$隨機碰撞到互質的分子分母的概率就大有不同，可以看看$n$的質因數，找幾個並非$n$的質因數，與$n$乘起來看看鹹淡，挑一個比較合理的就可以。

但是大家也不用因此沮喪，還是看看圖像吧。

就有以下的圖像

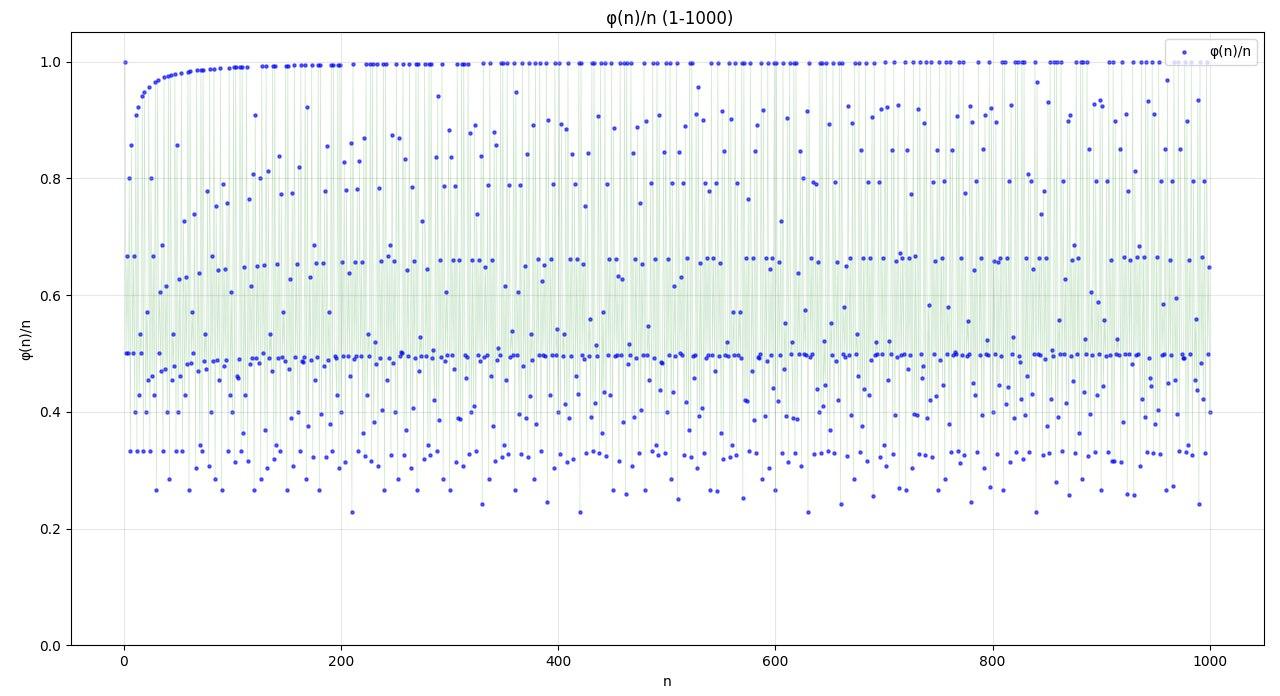
或許範圍可以大一些

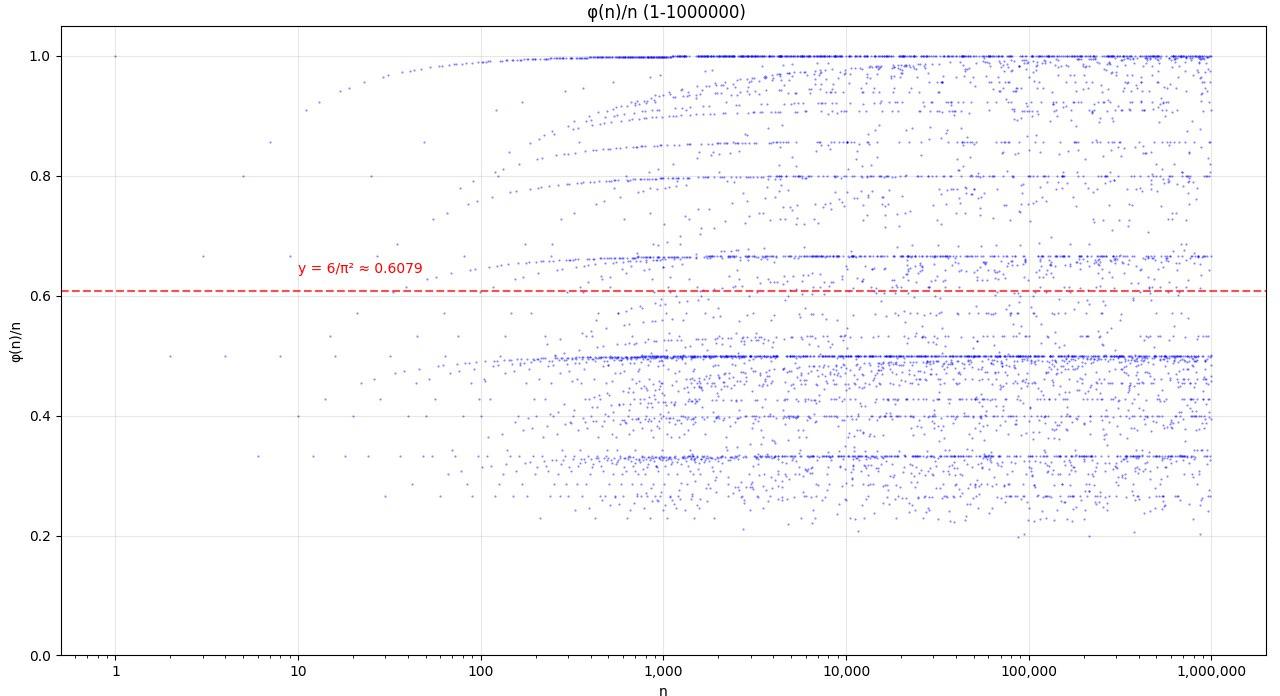
這樣看得就清楚多了。

可以看到，圖像呈現明顯的分形特性和自相似模式，可以觀察到多個周期性下降的結構，每條 "支線" 對應特定質數的倍數，隨著 n 增大，整體趨勢呈下降波動，而且隨著 n 增大，φ(n)/n 的平均值趨近於 6/π² ≈ 0.6079，這個結果與素數分佈的漸近密度相關。（以上是 AI 生成）

由此可見，既然碰撞概率下降不明顯，總而言之這個方法還是比較可信的，可以輕鬆發現一些沒什麼誠意的造假。

缺陷#

當然這個方法也是有缺陷的，出了上文提到的不嚴謹之處，由於通常的問卷調查結果是保留兩位小數的百分數，所以本代碼對誤差的 tolerance 在 0.0001，如果問卷數量超過 10000 份，得出的結果也只有 10000，能力就限制到這兒了。如果結果是保留一位小數的百分數，tolerance 在 0.001，那就是上限 1000 份，以此類推了。

此外窮舉優雅性不足，本來讓 AI 寫了一個連分數的算法，結果沒過測試，部分情況算出來的數字偏大，反正只有 10000 個數字，都用 python 了，就別追求效率，窮舉就完了。

最後還有一個缺陷，但我是不會說的，那不是增加我的發現難度嗎！

最後用一些知網的文獻練練手，讓大家看看到底準不準。

OK，收工。

此文由 Mix Space 同步更新至 xLog 原始鏈接為 https://www.actorr.cn/posts/default/Eulerstotient